A long time ago in a galaxy far, far away, two black holes circled each other with vicious intent. The black holes were destined for a cataclysmic union that would unleash more power than is released in the form of light from the rest of the universe combined! All of this power was in the form of gravitational waves, ripples in the very fabric of spacetime, that arrived on Earth on September 14, 2015. The signal was received by the twin LIGO (Laser Interferometer Gravitational-Wave Observatory) detectors,1 ushering in the era of gravitational wave astronomy—where precise instruments combine with accurate models to bring us new insights about our universe.

Artist’s rendition of two merging black holes similar to those detected by LIGO
Modified from LIGO/Caltech/MIT/Sonoma State (Aurore Simonnet)
But what exactly are gravitational waves? Gravitational waves solve an old problem with Newton’s law of gravitation. While this simple law describes nearly all gravitational effects we see in everyday life, it has a fundamental flaw: it describes gravity as an instantaneous force. In this framework, if the Sun were to suddenly vanish, the Earth would immediately stop orbiting and move in a straight line with its current velocity. Einstein realized that this would violate special relativity, which says that no force can be transmitted faster than the speed of light. But according to Newtonian gravity, the Earth would instantaneously react to the Sun’s disappearance.

From the film Testing Einstein's Universe by Norbert Bartel
This fundamental flaw is resolved by Einstein’s general relativity, a geometric theory describing how gravity arises from the curvature of spacetime, the 4-dimensional fabric of the universe. According to general relativity, if the Sun were to disappear, this information would be transmitted in the form of ripples in the curvature: gravitational waves. These waves travel at the same speed as light, thus keeping special relativity intact.
Einstein’s theory also tells us that gravitational waves are incredibly tiny and interact weakly with matter. They cause distortions in the LIGO detector of about 10-18 meters, which is 10 trillion times smaller than the width of a human hair! This weakness is both a blessing and a curse. The weak interactions with matter allow the waves to travel through the universe nearly unaffected, giving us clean information about their sources. In contrast, light, our primary source of information about objects in the universe, gets scattered and contaminated by interstellar dust and our own atmosphere. But the weakness of gravitational waves also makes them very hard to observe. To be detectable on Earth, they need to be generated by extremely compact, massive objects moving at high velocities, such as two black holes orbiting each other.
Gravitational waves from such a binary black hole were detected for the first time by LIGO in 2015, nearly a hundred years after Einstein’s prediction. This was the culmination of decades of experimental, theoretical, and computational advancements with important contributions from over a thousand scientists. Caltech’s own Kip Thorne and Barry Barish, along with MIT’s Rai Weiss, were awarded the 2017 Nobel Prize in Physics for this achievement. LIGO’s detection launched the field of gravitational wave astronomy and marked the opening of a never-before accessible window to the universe.
One of the goals of gravitational wave astronomy is to test general relativity. While general relativity is the current best description of gravity, it is likely an incomplete theory, as it is incompatible with quantum mechanics. Therefore, one might expect general relativity to break down in certain extreme conditions. Just before the black holes collide, they are moving at about half the speed of light, and the gravity is extreme. This is the most curved that spacetime gets throughout all the universe, except for during the Big Bang. Therefore, gravitational waves from a black hole merger provide the most stringent tests of general relativity.
Despite their exotic nature, black holes are remarkably simple objects. An astrophysical black hole is entirely characterized by its mass and spin. The renowned physicist John Wheeler famously said, “Black holes have no hair.” This means all other information—the “hair”—is forever lost in the black hole and is inaccessible to external observers. Thus, we can use nature as our particle accelerator: two accelerated black holes smash into each other and a single final black hole emerges. The masses and spins of the initial black holes, as well as the final black hole, can be inferred from the gravitational waves and we can test if they are consistent with general relativity.
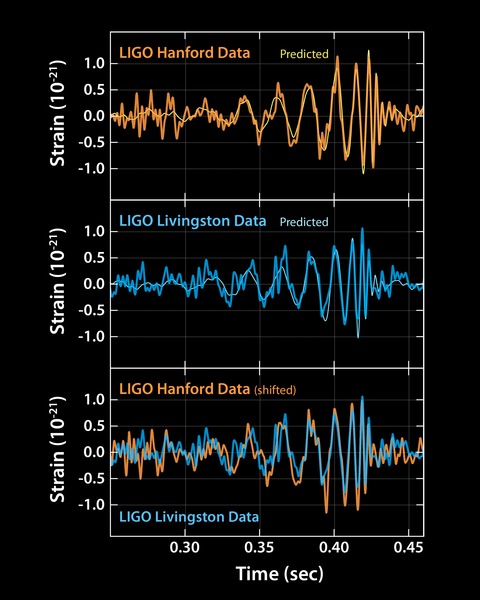
The data received at the LIGO detectors, along with the predicted shapes for the gravitational wave for the first detection
These tests require an accurate prediction of the gravitational waves and the final black hole, which involves solving Einstein’s equations. Unfortunately, solutions to Einstein’s equations are hard to come by, and for the problem of two black holes orbiting each other, there is no known exact, analytical solution, which is what mathematicians call the kind of solution you can write down with a pen and paper. Approximate analytical solutions can describe black holes that are far away from each other. These methods, however, break down near the merger due to the high velocities and extreme gravity, and we are left with only one option: simulating the black holes on a computer by numerically solving Einstein’s equations. The first successful numerical simulation of a black hole merger was achieved by Frans Pretorius in 2005,2 right here at Caltech, after decades of development. In the years since, various advances have filled in some missing pieces, but Pretorius’s numerical simulations essentially solved the binary black hole problem in general relativity!
Numerical simulation of the first LIGO detection
Simulating eXtreme Spacetimes, Max Planck Institute for Gravitational Physics
So, can we just use these numerical simulations to test general relativity against the gravitational waves observed by LIGO? There is still one problem: these simulations are very expensive! Even with state-of-the-art code developed by the Simulating eXtreme Spacetimes (SXS) collaboration,3 each simulation can take a month on a supercomputer. This is far too slow for direct use with LIGO. LIGO needs a model that can be rapidly evaluated with different values for variables, like the masses and spins of the black holes. Comparing these evaluations to the detected signal, one can identify the masses and spins of the source. This procedure, however, can require about 10 million evaluations, and would take about a million years to generate enough simulations!
As a result, the gravitational wave community uses approximate models that are much faster to evaluate, instead of full numerical simulations. For example, one might assume an underlying formula for the amplitude and frequency of the gravitational waves as a function of time, using physical intuition and analytical models that are valid when the black holes are far away from each other. Corrections are then added to the formula by calibrating to numerical simulations. Such calibrated models were used to analyze the signal from the first detection. These models were shown to be accurate enough for current LIGO sensitivity, but they can break down as detectors become more sensitive and the approximations no longer hold.
Thus, an important question remains: can we build a model which does not need to make any such approximations, but is still fast enough to keep up with LIGO’s needs? This is the domain of surrogate modeling, where we make new predictions by interpolating between existing numerical simulations. Using tools similar to machine learning, we train our surrogate models against the simulations and learn from the data how different black hole mergers generate gravitational waves with different amplitude and frequency. While these models are currently restricted to nearly equal masses and moderate spins, they are the most accurate models available.4,5 In fact, they have been shown to be as accurate as the simulations themselves, while only taking a fraction of a second to evaluate. This means that you never have to do a new simulation, at least for masses and spins where these models are valid.
Apart from their use in analyzing gravitational wave data, there is another very cool application of surrogate models: movies! Binary black hole systems are highly dynamical and complex, making it hard to model or develop intuition about them. In particular, if the spins of the black holes are misaligned with respect to the orbital angular momentum, the spins interact with the orbit and cause the system to wobble. Visualizing numerical simulations provides a valuable means to gain insights about these systems by allowing you to see the wobble. However, visualizations like the one above usually require expensive simulations on a supercomputer. Now that we have surrogate models that accurately reproduce the simulations, we developed software,6 written in the popular programming language Python, that lets you generate a visualization like the one below in a few seconds on your laptop!
Visualization of binary black holes using surrogate models. This shows the merger of a 20 solar-mass black hole with a 40 solar-mass black hole. The black holes' spins are indicated with arrows—because they are misaligned with respect to the orbital angular momentum (pink arrow), the orbit wobbles, or precesses. For more information, see our binary black hole explorer.
Vijay Varma
LIGO, now joined by its sister detector Virgo, has been going strong since the first detection. The current number of detections stands at 11! In the future, detectors will become much more sensitive, and detections are expected to become routine. This influx of new data will also allow more precise tests of general relativity. Accurate and fast models such as surrogate models will play a key role as we head into the era of high-precision gravitational wave astronomy. When Galileo turned his telescope to the sky, it marked the beginning of modern electromagnetic astronomy, a field which revealed a menagerie of unexpected cosmic wonders such as quasars, pulsars, cosmic microwave background, gamma-ray bursts, and much more. What new wonders does the field of gravitational wave astronomy hold for us?
References
1: Abbott, B. P. et al. Phys. Rev. Letters, 2016.
2: Pretorius, F. Phys. Rev. Letters, 2005.
3: Simulating eXtreme Spacetimes
4: Blackman, J. et al. Phys. Rev. D, 2017